What is Active Matter?
Published:
Active matter is a class of non-equilibrium systems where time reversal symmetry is broken at the microscopic scales. We will explore what this means in this blog post.
Time reversal symmetry breaking
In statistical physics we often say this system is in equilibrium and that system is out-of-equilibrium et cetera. But what is equilibrium? and what is out-of-equilibrium?
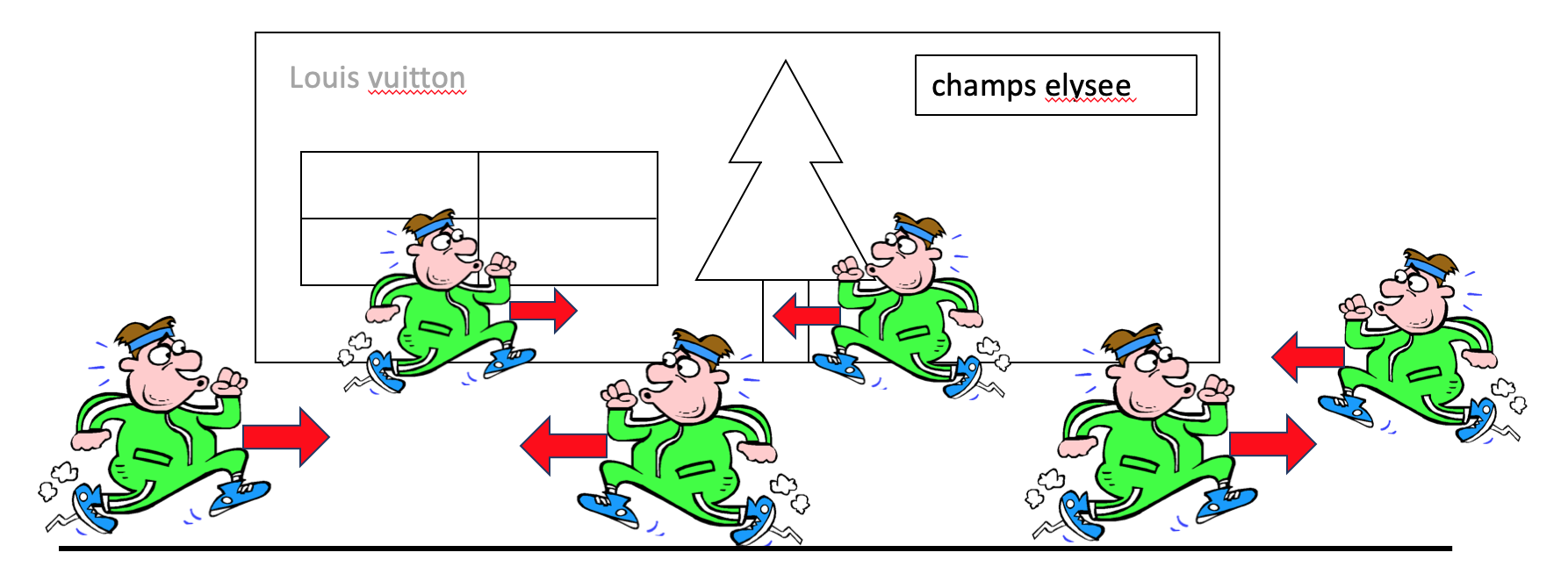
We say that a system is in equilibrium if it respects time reversal symmetry (TRS) at steady state and out-of-equilibrium if it violates TRS at steady state. For example, consider the pedestrations on Champs Elysee. They clearly constitute a non-equilibrium system because if we watch the movie backwards they will appear to walk backwards.
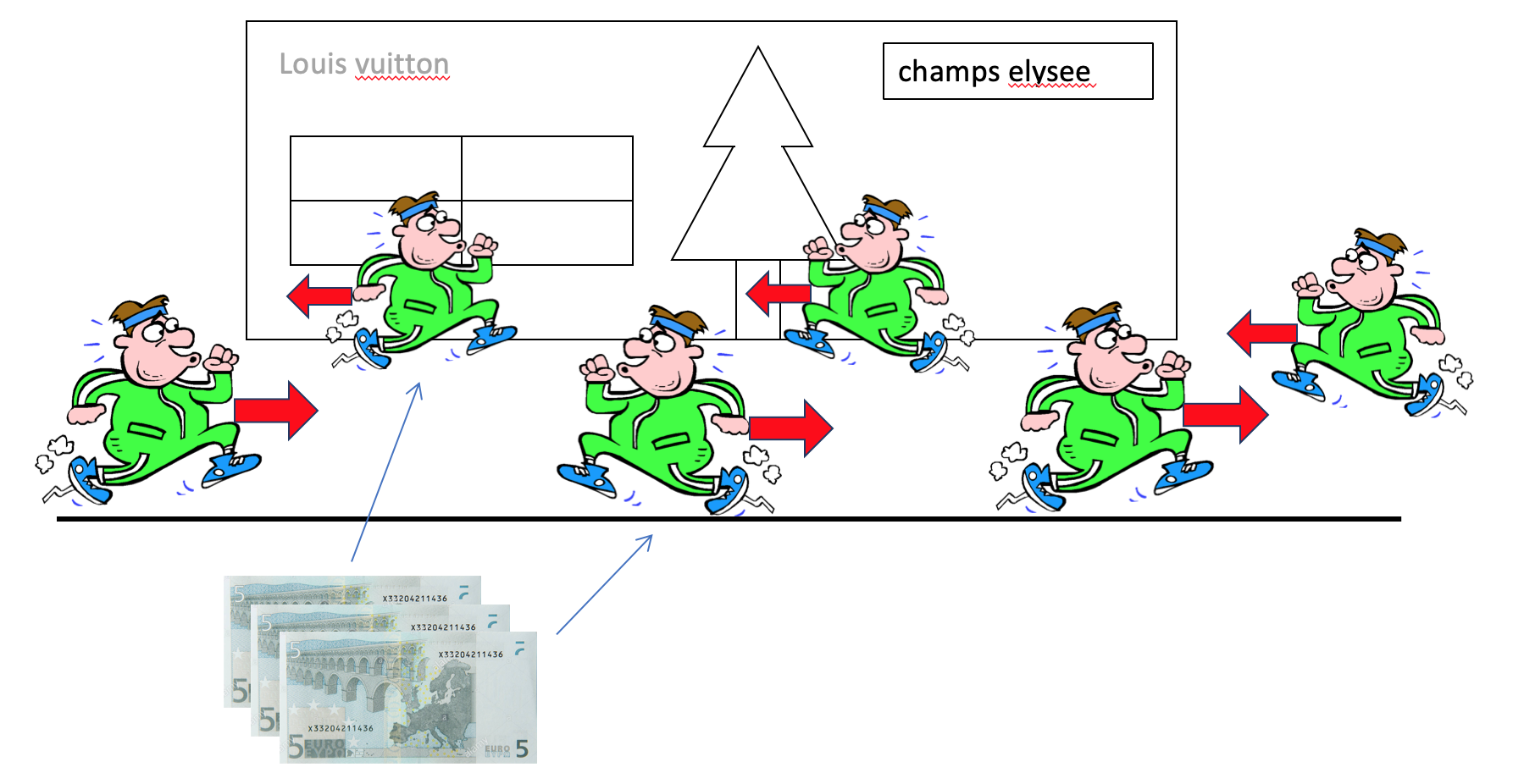
But now suppose we pay half the people 5€ each to walk backwards. They now become an equilibrium system because if we watch the movie backwards they look the same (statistically).
Active field theories
Probably we are familiar with the Cahn-Hiliard equation:
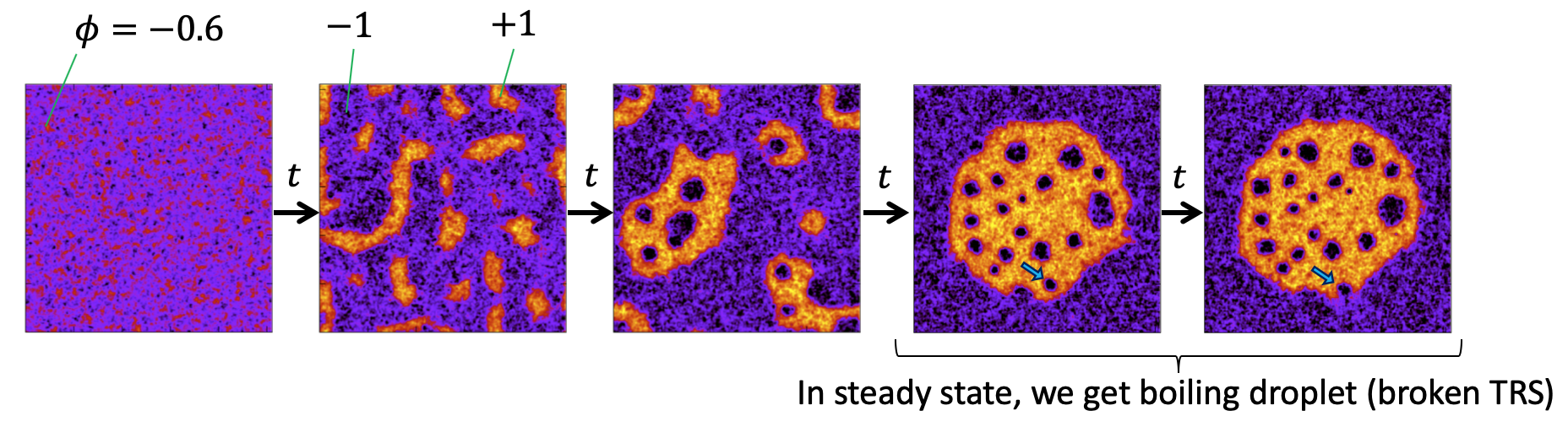
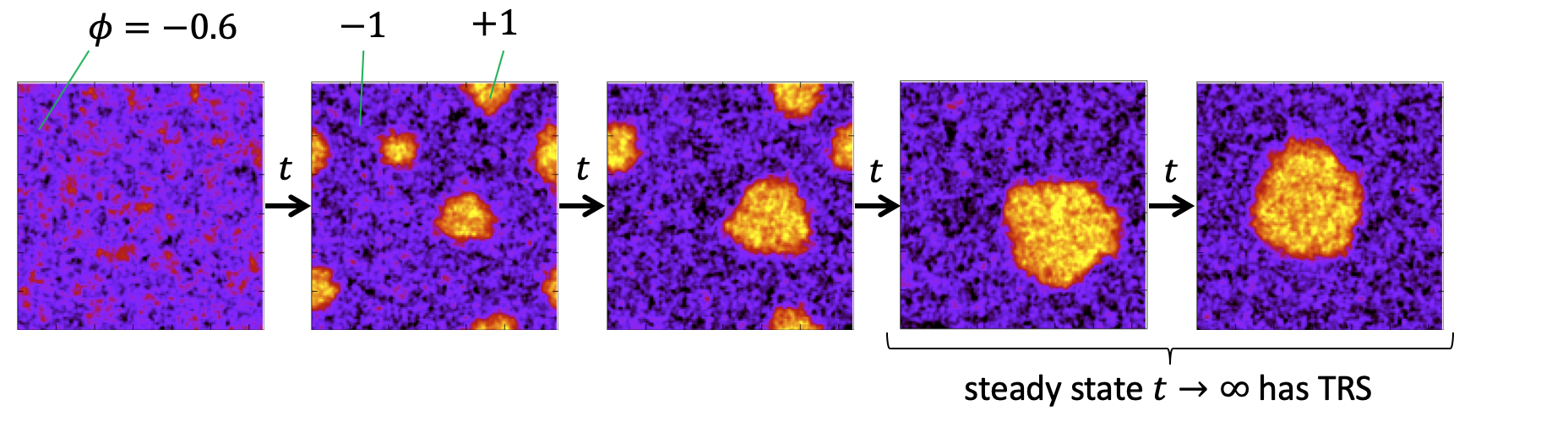
\[\frac{\partial\phi}{\partial t} + \nabla\cdot\left(-\nabla\frac{\delta F}{\delta\phi} + \boldsymbol{\Lambda}\right) = 0\]In the equation above, $\phi$ is the density of the fluid. If we start from a homogenous density $\phi = -0.6$, the system will phase-separate into high density $\phi = +1$ (liquid) and low density $\phi = -1$ (vapour) phase. In steady state $t = \infty$, we end up with a single big blob of liquid.
Introducing the non-equilibrium Cahn-Hiliard equation (also called active model B+)….
\[\frac{\partial\phi}{\partial t} + \nabla\cdot\left( -\nabla\frac{\delta F}{\delta\phi} + \boldsymbol{\Lambda} + \lambda\nabla|\nabla\phi|^2 + \zeta(\nabla^2\phi)\nabla\phi \right) = 0\]If we start from the same intial configuration, we see similar phenomena where the fluid phase-separate into high density and low density. However in the steady state, we get a boiling droplet. The droplet is in perpetual boiling state (see movie at the end), which is not possible in equilibrium because all the liquid will be evaporated.