Statistical Physics of Soft Condensed Matter

This is a graduate course in Statistical Physics and Soft Condensed Matter. This course is aimed at PhD students and postdocs who are going to do research in Theoretical Soft Condensed Matter Physics and Statistical Physics.

0. Introduction

This course is an evolution of the Part III course in Cambridge of the same name, given by Prof. Cates, but with the added computational aspects. This course assumes some knowledge of Python (see Python Crash Course for reference). Entire course is written in Jupyter notebook.

1. Brownian motion

Brownian motion is the jittery motion of micron-sized particles in a fluid. These particles do not sit still and instead they are being bombarded by even smaller fluid molecules. These random kicks from the fluid molecules can be approximated as random force, which we will model below mathematically as a stochastic process.

1.1. Langevin equation

(Work in progress.)

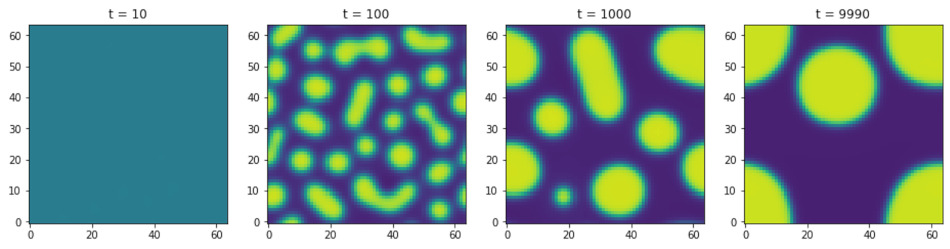
2. Binary fluid

In this section, we will start with the Cahn-Hilliard equation, which is a model for phase-separation in a binary fluid, e.g. water/oil phase separation, liquid/gas phase separation, and so on. Then we will extend the Cahn-Hiliard equation to include momentum conservation (Cahn-Hilliard-Navier-Stokes equation) and noise (model B equation) to model droplet dynamics, droplet evaporation, microfluidics, and so on.

2.1. Cahn-Hiliard equation

In this tutorial, we will introduce the order parameter, the coarse-grained free energy and the time evolution of the order parameter. We will also look at the equilibrium phase diagram and the linear stability analysis of the homogenous phase. The link to the jupyter notebook is here: Cahn-Hiliard notebook.

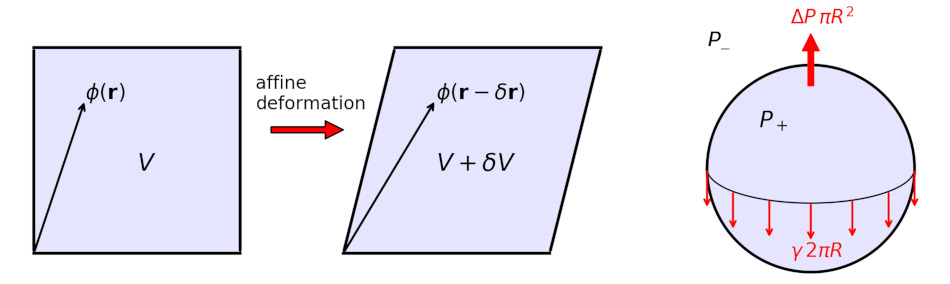
2.2. Droplet

In this tutorial, we will derive the macroscopic properties of a droplet, such as surface tension, pressure, contact angle etc, from the free energy. The link to the jupyter notebook is here: droplet notebook.

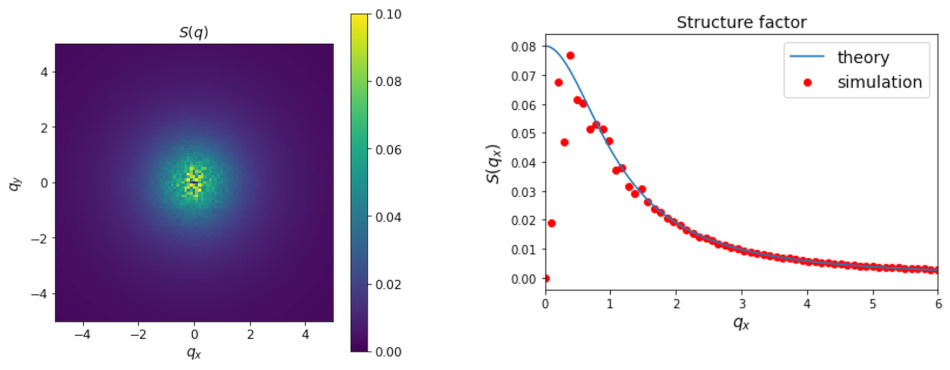
2.3. Adding noise (equilibrium model B)

When the droplets are very small (~microns), thermal fluctuations become important. For instance, the droplet might undergo a Brownian motion like the colloidal particle described in the previous section. In this tutorial, we will add thermal noise to the Cahn-Hiliard equation and study the statistics of this noisy dynamics. The link to the jupyter notebook is here: model B notebook.